Return Stacked® Academic Review
Explaining Momentum Strategies Using Intrinsic Price Fluctuations
Authors
A. N. Baltas
SSRN Working Paper Series, December 2011
Explaining Momentum Strategies Using Intrinsic Price Fluctuations
Key Topics
return stacking, portfolio construction, risk management, capital efficiency, momentum, trend following, portable alpha
Decoding the Momentum Effect Through Price Decomposition
The momentum effect, where stocks that have performed well recently tend to continue performing well and vice versa, is a cornerstone of quantitative finance. In “Explaining Momentum Strategies Using Intrinsic Price Fluctuations,” A. N. Baltas delves into this phenomenon by decomposing stock prices into intrinsic modes. Utilizing Empirical Mode Decomposition (EMD), the study breaks down price movements into a long-term trend and a series of short-term oscillations. This approach provides a nuanced understanding of how different price components contribute to the success of momentum strategies.
Baltas analyzes data from NYSE, AMEX, and NASDAQ stocks over the period from 1962 to 2008. The study reveals that momentum profits are most pronounced in stocks exhibiting high short-term variability but low long-term variability. This suggests that momentum is influenced not just by persistent trends but also by the nature of price fluctuations across different time horizons. By identifying an optimal holding period of six months, the research balances return maximization with the minimization of transaction costs.
Impact of Transaction Costs and Risk Management
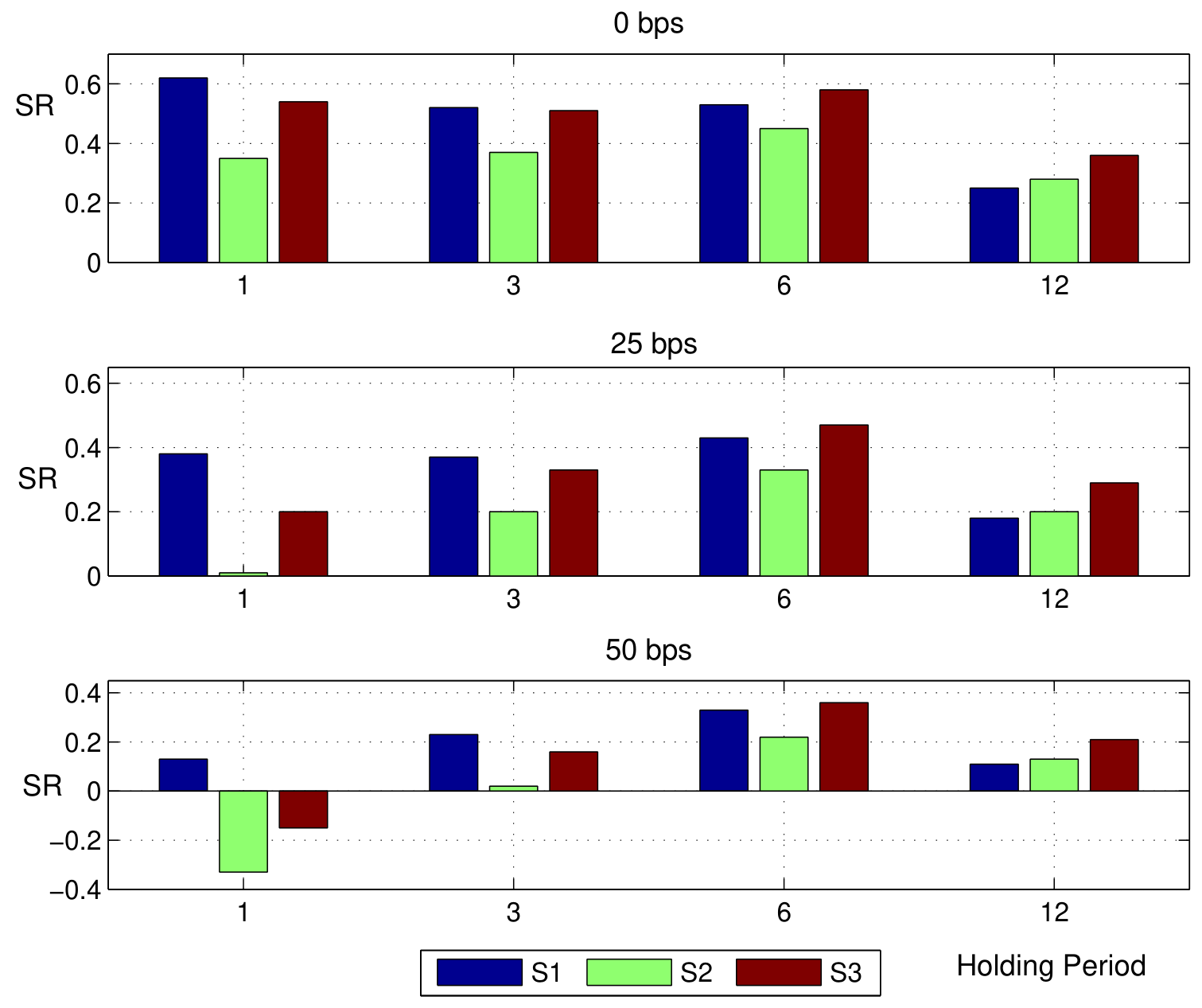
Figure 1: The Effect of Transaction Costs on the Sharpe Ratio (Original: Figure 5)
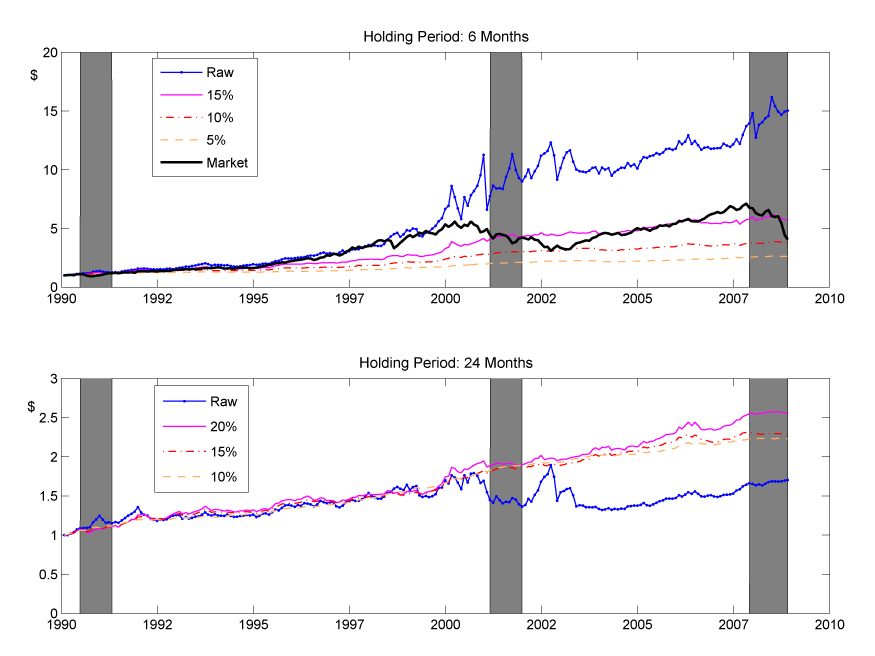
Figure 2: Dollar Growth for the Double-Sort Trend/Fluctuation Strategy with Stop-Loss Rules (Original: Figure 6)
Integrating Momentum Insights into Return Stacking Strategies
Baltas’s insights have significant implications for return stacking strategies, which aim to enhance diversification and capital efficiency by combining multiple sources of return within a single portfolio. Understanding the interplay between trends and oscillations in price movements can inform the construction of diversified portfolios that harness alternative risk premia.
For instance, incorporating momentum strategies with optimal holding periods can be synergistic when combined with trend following approaches in a return stacking framework. By aligning the investment horizons and managing transaction costs, investors can achieve a more efficient portfolio. Similarly, the research on stop-loss rules aligns with the principles of portable alpha, where leveraging uncorrelated strategies can enhance returns without proportionally increasing risk.
The emphasis on risk management techniques, such as stop-loss thresholds, is particularly relevant when combining strategies like momentum with carry futures yield. Effective risk controls can mitigate drawdowns and contribute to more stable returns, which is a key objective in return stacking portfolios.
Key Takeaways
- Optimal Holding Period: A six-month holding period balances return maximization with transaction cost minimization.
- Transaction Costs Impact: Higher transaction costs significantly reduce risk-adjusted returns, especially for shorter holding periods.
- Risk Management Benefits: Applying stop-loss rules enhances performance and reduces volatility, emphasizing the importance of risk controls.