Trend-following is a popular investment approach that seeks to capitalize on market momentum by buying assets that are rising and selling those that are falling. While many studies have demonstrated the potential of trend-following strategies to generate attractive returns, they often overlook the significant impact of transaction costs associated with frequent trading. Valeriy Zakamulin and Javier Giner, in their paper “Optimal Trend-Following With Transaction Costs,” address this gap by developing a new model that optimizes trend-following strategies while explicitly accounting for transaction costs.

The authors recognize that transaction costs are an inevitable part of trading that can erode the profitability of trend-following strategies, especially those that require frequent rebalancing. To tackle this challenge, they propose a heuristic control approach that simplifies the optimization problem by restricting it to moving average crossover rules. This method avoids the complexity of stochastic optimal control theory and makes the findings more accessible and practical for investment professionals.

By assuming that financial asset returns follow an autoregressive process (AR(*p*)), the authors derive analytical solutions for expected transaction costs, expected returns, and the Sharpe ratio of trend-following strategies in the presence of transaction costs. These solutions enable the use of standard optimization techniques to determine the optimal return weights for a given trend-following indicator.

One of the significant contributions of Zakamulin and Giner’s paper is demonstrating that moving average crossover rules can effectively approximate the optimal solutions for trend-following strategies when considering transaction costs. This provides theoretical support for the widespread use of moving average crossovers in practice, which, until now, lacked a robust theoretical foundation.

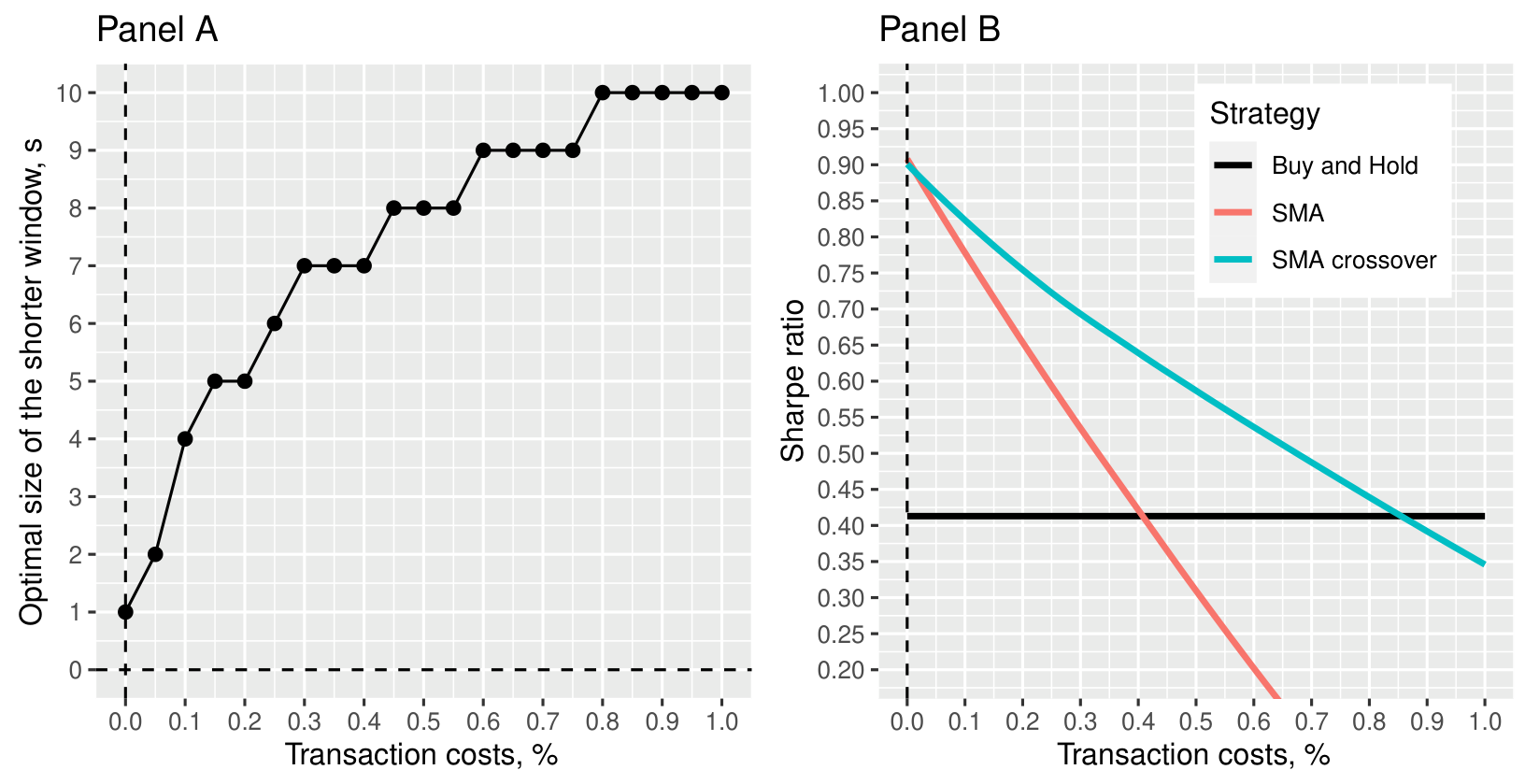
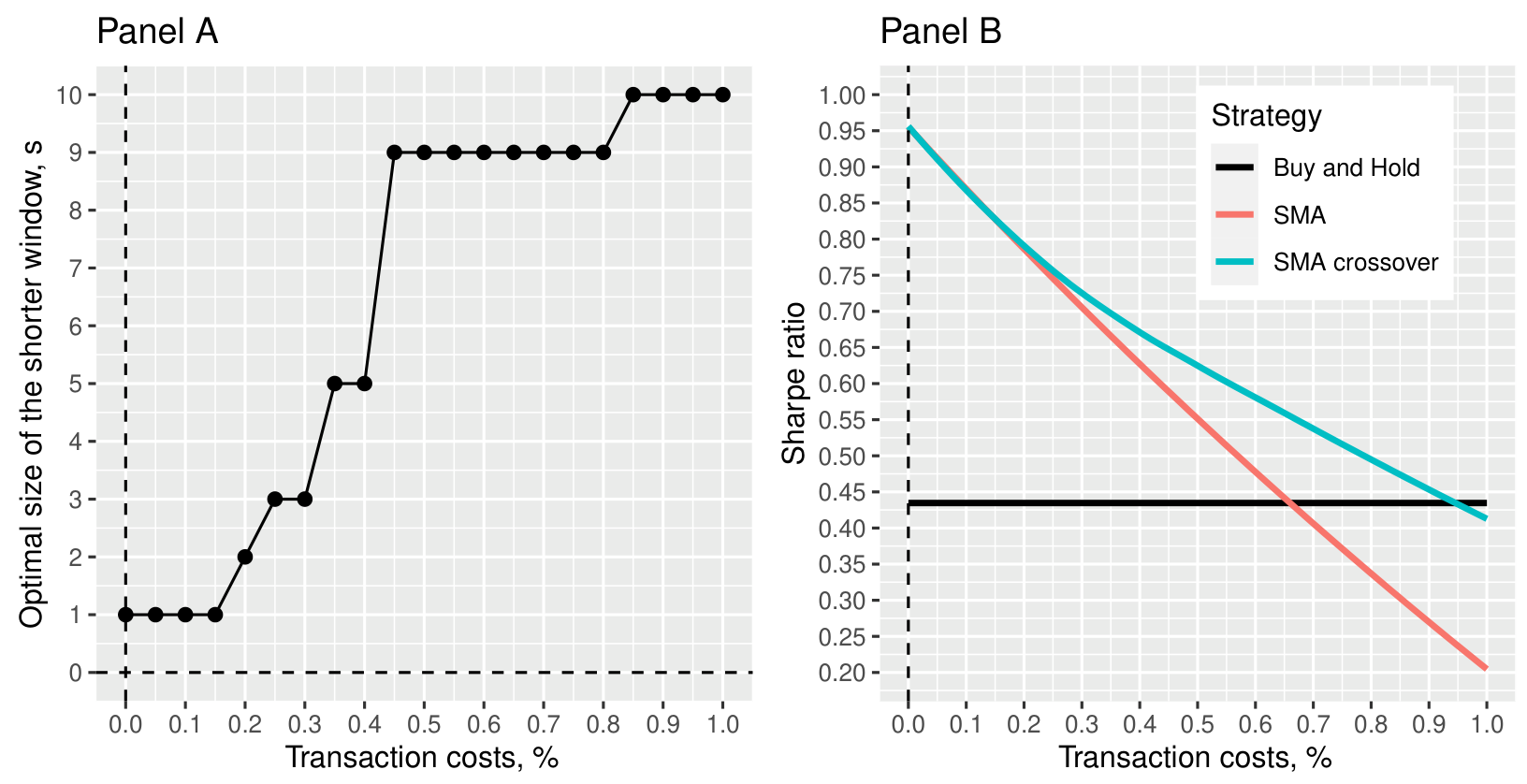
A critical insight from their analysis is the relationship between transaction costs and the optimal lookback periods of trend-following strategies. The authors find that as transaction costs increase, the optimal lookback period tends to lengthen. This finding suggests that in environments with higher transaction costs, investors should adopt a more measured approach by using longer lookback periods to reduce trading frequency and enhance capital efficiency.

Figure 1: Panel A plots the optimal size of the shorter window in the s- and 25-day simple moving average (SMA) crossover rule versus the level of proportional transaction costs (τ). Panel B plots the Sharpe ratio of the optimal s- and 25-day SMA crossover rule, the Sharpe ratio of the 25-day SMA rule, and the Sharpe ratio of the buy-and-hold strategy versus τ. It is assumed that daily returns follow an AR(25) process with linearly decreasing autoregressive coefficients and a trend strength κ = 0.35. Other parameters: mean annual return μ = 15.5%, standard deviation σ = 27%, and risk-free rate rₑ = 4%.

Figure 1 illustrates how the optimal size of the shorter moving average window increases as transaction costs rise (Panel A). This indicates that when trading costs are higher, using a longer lookback period for the shorter moving average helps reduce trading frequency and transaction costs. Panel B shows that the Sharpe ratio of the optimal SMA crossover strategy remains higher than that of both the standard 25-day SMA rule and the buy-and-hold strategy across various levels of transaction costs. This demonstrates the advantage of optimizing the trend-following strategy by adjusting lookback periods in response to transaction costs.

Figure 2: Panel A plots the optimal size of the shorter window in the s- and 25-day SMA crossover rule versus τ, based on historical returns of a small-cap stock portfolio from 1952 to 2021. Panel B plots the Sharpe ratio of the optimal s- and 25-day SMA crossover rule, the Sharpe ratio of the 25-day SMA rule, and the Sharpe ratio of the buy-and-hold strategy versus τ using the same dataset.

Figure 2 provides empirical validation of the theoretical findings using historical data. Panel A shows that the optimal window size increases in steps as transaction costs rise, reaffirming the need to adjust lookback periods in response to transaction costs. Panel B illustrates that the optimized SMA crossover strategy consistently outperforms the standard 25-day SMA rule and the buy-and-hold strategy across different transaction cost levels, as measured by the Sharpe ratio.

The insights from Zakamulin and Giner’s research have important implications for return stacking strategies, which aim to enhance portfolio performance by efficiently combining multiple return streams using leverage without significantly increasing risk. Return stacking relies on integrating diversifying strategies, such as managed futures and trend-following, alongside traditional equities and bonds to improve capital efficiency and diversification. Learn more about return stacking and its evolution in portfolio construction here.

In managed futures, trend-following strategies are a core component, capitalizing on persistent price movements across various asset classes. Incorporating optimized trend-following strategies that account for transaction costs is crucial for enhancing the risk-adjusted returns of return stacked portfolios. By adjusting the lookback periods in response to transaction costs, investors can reduce unnecessary trading, lower costs, and improve capital efficiency. This aligns with the principles of portable alpha, where alpha generated from one strategy (e.g., optimized trend-following) can be efficiently combined with other return sources in a portfolio.

Moreover, optimizing trend-following strategies with longer lookback periods in high transaction cost environments can enhance the yield and performance of return stacked portfolios. By improving the net performance of the managed futures component, investors can unlock additional diversification benefits and better manage risk. For more on managed futures and trend-following strategies, visit this article.

Zakamulin and Giner’s paper provides a valuable framework for optimizing trend-following strategies by explicitly accounting for transaction costs. Their findings highlight the importance of adjusting lookback periods based on the level of transaction costs to improve capital efficiency and enhance risk-adjusted performance. By demonstrating that moving average crossover rules can approximate optimal solutions, the authors offer practical guidance for investors implementing trend-following strategies.

These insights are particularly relevant for return stacking and managed futures strategies, where efficient use of capital and cost management are essential. By integrating optimized trend-following strategies into return stacked portfolios, investors can achieve better diversification, harness portable alpha, and improve overall portfolio construction. Accounting for transaction costs not only enhances net performance but also contributes to more robust risk management, allowing investors to unlock the full potential of trend-following strategies in a cost-effective manner.