Stacking in a Higher Interest Rate Environment
Overview
This article explores the relevance of leverage in investment strategies amid higher interest rates. The decision to use leverage, through methods like return stacking or portable alpha, should be based on the expected returns of assets rather than current interest rates. By emphasizing the importance of understanding risk premiums, we highlight that leverage can remain beneficial even in environments with higher interest rates.
Key Topics
Return Stacking, Portable Alpha, Capital Efficiency, Interest Rates
Introduction
Coming out of a decade-long low interest rate environment, many investors are questioning whether utilizing leverage remains a prudent idea now that interest rates are meaningfully above zero.
Our answer is that the decision to utilize leverage, through methods like return stacking or portable alpha, should be based on expected returns of assets rather than current interest rates. If leverage makes sense in a low-interest rate environment, then it should make sense in a high interest rate environment.
Risk Premiums and the Risk-Free Rate
At the foundation of any discussion about return is the risk-free (RF) rate, which is the rate of return earned for investing in a theoretical, riskless asset. Although the risk-free rate doesn’t actually exist, a typical proxy is the yield of U.S. Treasuries, since those are as close to “risk-free” as an investor can get.
Intuitively, for any investor to make an investment in anything that is not riskless, they would require the expected return on that investment to be higher than the risk-free rate (this is not strictly true, as insurance instruments offer an obvious counter-point, but is sufficiently true for most investments). Put simply: the investor expects to get paid to be willing to bear the risk. As we have been known to say, “No Pain, No Premium.” Generally speaking, if a risky asset has an expected return lower than the risk-free rate, the price of that asset should come down such that the expected return goes up and properly compensates the investor for the risk taken.
For any asset, the expected return above the risk-free rate is called a “risk premium.” For example, in equities we have the “Equity Risk Premium” (ERP) and in bonds, we have the “Term Risk Premium” (TRP). (There are many other risk premiums that we could list, but to keep this article succinct, we will focus on the ERP and TRP.)
Figure 1: Expected Returns on Cash, Bonds, and Equities
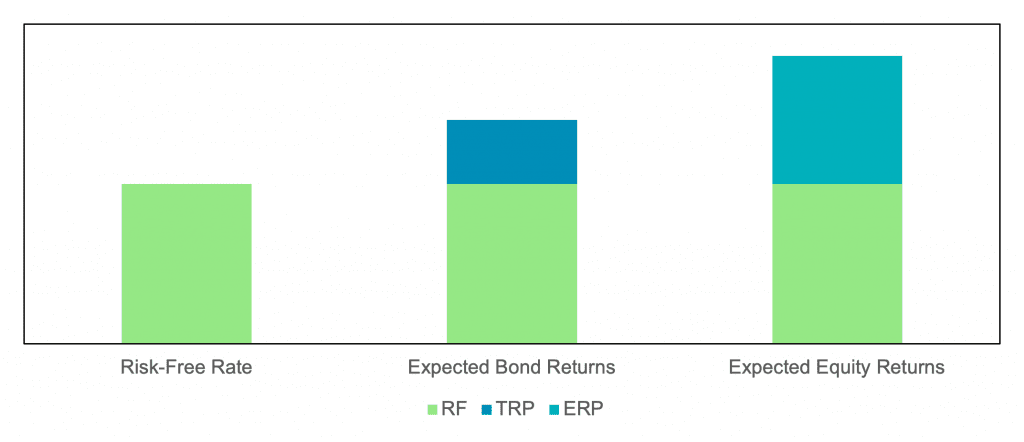
Source: Newfound Research. For illustrative purposes only. Consult your financial advisor before making any financial decisions.
From Figure 1, we can see that the expected returns for bonds and equities are composed of both the risk-free rate and their respective risk premiums. These risk premiums are defined as the expected excess return of the asset above the risk-free rate.
Approaches like return stacking or portable alpha aim to capture these risk premiums by overlaying alpha-generating strategies on top of beta exposure.
Applying Leverage to an Asset
If an investor wants to gain exposure to the S&P 500 index, most investors will operate in the cash market, using cash to purchase shares of the SPDR S&P 500 ETF Trust (ticker: SPY) or the underlying stocks themselves.
Another method, however, could be to borrow money (using leverage) to purchase the exposure. If we borrow the money, we will have to pay back the borrowed amount plus the interest accrued, but we would keep whatever we made in excess of that amount. So, if the S&P 500 returns more than the interest we must pay, we come out ahead by borrowing. In this scenario, the excess return of the S&P 500 is what we expect to make by borrowing, so long as the investor can borrow close to the risk-free rate.
This latter method is effectively how an S&P 500 futures contract works.
One minor difference that we would be remiss to not mention is the interest rate. If an investor goes to a bank to borrow money, the interest rate charged would likely be significantly higher than the yield on U.S. Treasury Bills, while futures contracts embed an interest rate remarkably close to the yield on 1–3 month U.S. Treasuries.
Taken together, an investor who purchases an S&P 500 futures contract expects to earn the equity risk premium of equities, and their realized return will be equal to the return of the S&P 500 minus the risk-free rate (assuming the embedded borrowing cost in S&P 500 futures equals the risk-free rate).
Register for our Advisor Center
Tools Center:
Easily backtest & explore different return stacking concepts
Model Portfolios:
Return stacked allocations, commentary and guidance designed
for a range of client risk profiles and goals
Future Thinking:
Receive up-to-date insights into the world of return stacking theory and practice
Why Does that Matter
Since return stacking inherently uses leverage (typically via futures contracts) to stack returns into a portfolio, the risk premiums of the assets in the portfolio are of great interest to investors. However, what the section above hopefully illuminates is that the actual level of interest rates does not.
In fact, since the return of every asset can be decomposed into the risk-free rate and its excess return, and futures contracts effectively isolate the excess return, the choice whether to use leverage based upon the level of the risk-free rate implies that there is a relationship between the level of the risk-free rate and the size of the expected risk premium. In other words, it’s a market timing decision!
To further illustrate this, in Figure 3, we build a 100/100 stock/bond portfolio to analyze how the expected returns change as we introduce leverage to the portfolio.
Hypothetical Expected Return Decomposition of a 100/100 Portfolio
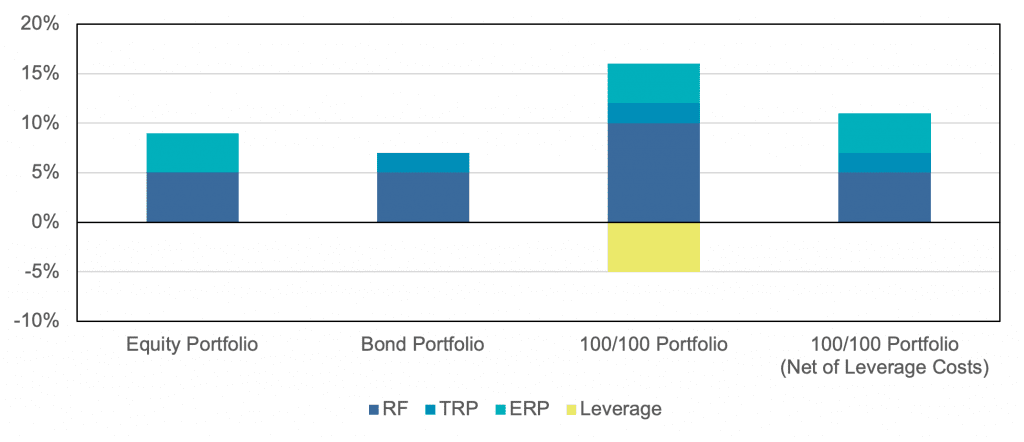
Source: Newfound Research. For illustrative purposes only. All expected returns are hypothetical and should not be relied on for investment decisions. This depiction assumes that the interest charged on leverage is equal to the risk-free rate, which may not be realistic. Consult your financial advisor before making any financial decisions.
From Figure 3, we can surmise that stacking bonds on an equity portfolio leaves the portfolio with three things: the risk-free rate, the ERP, and the TRP. Even though we are implicitly incurring borrow costs by applying leverage, we clear that hurdle so long as the ERP and/or the TRP are positive. Since we would expect risky assets to have a positive excess return, a logical conclusion is that the level of interest rates is inconsequential to applying leverage to capture these risk premiums.
The Return Stacking landscape is ever evolving, go deeper by connecting with a team member.
Do We Even Need to Talk about Leverage Here?
While strategies such as return stacking and portable alpha tend to apply the lens of leverage due to our affinity for return stacking, does this conversation even require the application of leverage?
The short answer is “no,” but the long answer utilizes a concept that we already applied earlier in this article.
If we assume that the risk-free rate is 5%, for us to hold any allocation to a risky asset then we need to have the expectation that that risky asset will return greater than 5%, or at least properly compensate the investor for the risk taken.
To further develop this intuition, let’s detail two potential investments:
- An investment that will return 5% in one year, guaranteed.
- An investment that will return a maximum of 5% in one year, with a 50% probability of losing 5%.
No rational investor would select the second option, as the first is guaranteed and provides the same maximum gain.
Without even applying leverage, the investor is better off allocating to the risk-free asset, since it is irrational to allocate to the second choice.
If an investor has the view that equities or bonds will underperform cash (i.e., the ERP or TRP are negative), then that investor should allocate to cash. This decision is true regardless of whether the position is levered or not.
If, however, the risk-free rate goes up and we believe that it is no longer prudent to use leverage, what we’re actually saying is, “because the risk-free rate went up, we believe the risk premiums of our assets have gone down.” Again, this is inherently a market timing decision based upon the level of the risk-free rate. (That is not to say that there isn’t a potential relationship between the risk-free rate and levels of risk premiums due to aggregate investor risk preferences, but they should be contemplated explicitly.)
Conclusion and Tying It All Together
To concretely summarize this post, we posit the following:
- Leveraged exposures should earn (approximately) the excess return of the asset class.
- The choice of whether to invest in an asset, through strategies like return stacking and portable alpha, should be driven by its expected risk premium and potential benefit to the portfolio as a whole.
- For higher interest rates to imply that leverage is no longer attractive, it must mean there exists a relationship between the level of interest rates and expected risk premiums. In other words, we must believe we can use the level of interest rates as a market timing signal!
Strategies like return stacking and portable alpha continue to empower investors to enhance returns through capital efficiency, regardless of the prevailing interest rate environment. By focusing on expected risk premiums and understanding the true drivers of returns, investors can make informed decisions that align with their long-term financial objectives.
Consult your financial advisor before making any financial decisions. Past performance is not indicative of future results.

